These Class 10 Maths Chapter 2 Exercise 2.1 Solutions are the best answers available on any website. You can effortlessly tackle the exercises presented in Class 10 Maths Chapter 2 Polynomials. Enhance your understanding of the fundamental mathematical concepts and theories explored in Chapter 2 Polynomials. Our platform also provides valuable guidance on crafting concise, word-efficient answers of optimal length. You can also watch problem solving videos for Class 10 Maths Chapter 2, in addition to the NCERT Solutions.

Use this link — 🌐 10.solutionsir.com for any kind of help in 10th class 2023-24. Click Here for » All Chapters: NCERT Solutions for Class 10 Maths.
Class 10 Maths Chapter 2 Exercise 2.1 Solutions
In this section of Chapter 2 “Polynomials“, you have studied the following points ⚡:
- Observe the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.
- For any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes, either open upwards or open downwards depending on whether a > 0 or a < 0. (These curves are called parabolas.)
- A polynomial of degree 2 has atmost two zeroes.
- A polynomial of degree 3 can have at most three zeroes.
- In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at atmost n points. Therefore, a polynomial p(x) of degree n has at most n zeroes.
In class 10 maths Chapter 2 Exercise 2.1 solutions, let’s try to find the answers to these questions —
EXERCISE 2.1
Question 1: The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
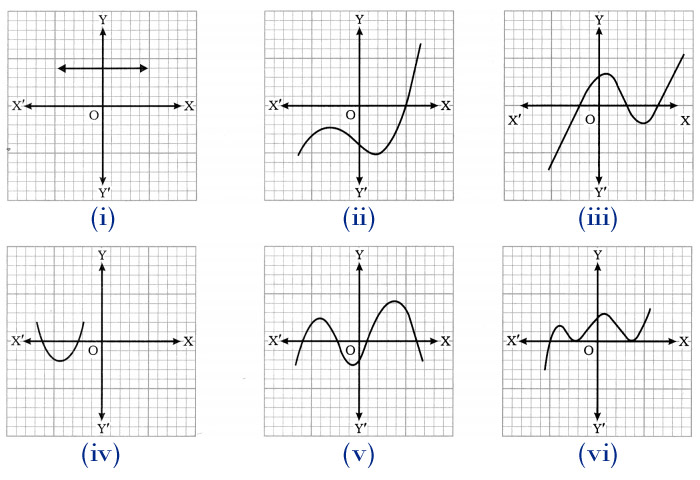
Answer 1: (i) The number of zeroes is 0 as the graph does not cut the x-axis at any point.
(ii) The number of zeroes is 1 as the graph intersects the x-axis at only 1 point.
(iii) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
(iv) The number of zeroes is 2 as the graph intersects the x-axis at 2 points.
(v) The number of zeroes is 4 as the graph intersects the x-axis at 4 points.
(vi) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.

